技術情報
微粒子技術コラム
応用編
応力数と応力強度について
応力モデルについて
応力モデルでは粉砕・解砕(分散)を「応力数」と「応力強度」で評価を行う1)、2)。応力数は粒子破壊を支配し、応力強度が大きいほど粒子破壊が効果的に進行する。また応力数と応力強度から比エネルギーも解析算出できる3~5)。
応力数
1. 応力数
応力数 SN は粒子がビーズから応力を受ける回数で、ビーズの接点数 NC とビーズの接触点間に粒子が入り込み応力が作用する確率 WB 、ビーズミル内の粒子数 NP により表される(式1)。
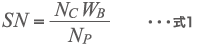
2. ビーズの接点数
ビーズの接点数 NC はアジテータの回転数 n [1/s] と粉砕時間(滞留時間) t [s]、ベッセル内に充填するビーズ数 NGM [-]に比例すると考えると式2となる。
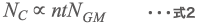
ここで、ベッセル内に充填するビーズ数 NGM [-]は、ベッセル容量 VGC [m3]とビーズ充填率ΦGM [-]、ビーズ充填時の空間率ε [-]、ビーズ径 dGM [m]により式3となる。
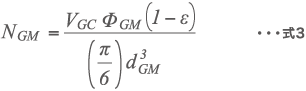
式3を式2に当てはめると式4となる。
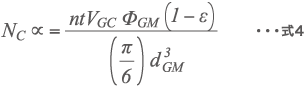
3. ビーズの接触点間に粒子が入り込み、応力が作用する確率
粒子はビーズとビーズの接触点にはさまれると粉砕されるので、ビーズの接触点間に粒子が入り込み応力が作用する確率 WB は、ビーズ径 dGM [m]に比例すると考えられる (式5) 。
凝集体の解砕では大きな応力は必要なく、ビーズ同士の面で十分なため式6となる。
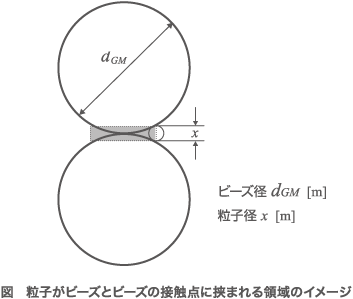
粉砕を例に、ビーズの間に粒子が挟まれる領域を図に示した。
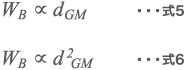
4. ビーズミル内の粒子数
ビーズミル内の粒子数 NP はビーズミル内の粒子の量(体積) VPtot [m3]と粒子の量(体積) VP [m3]、固形分容積濃度 CV [-]、ベッセル有効容量 VGC [m3]とビーズ充填率 ΦGM [-]、ビーズ充填時の空間率 ε [-]により式7で示される。
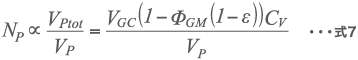
まとめると応力数 SN は式4と式7から算出できる。また、粉砕では式5が式8とも表すことができ、解砕の場合は式6から式9になる。
粉砕の場合の応力数
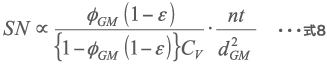
解砕の場合の応力数
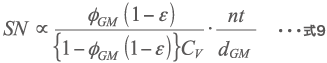
応力強度
応力強度は粒子がビーズから受ける応力エネルギーの大きさである。ベッセル内のビーズは均等な動きではなく、アジテータの先端部が最も応力強度が高くなる。応力強度 SI は式10で示される。
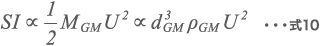
アジテータ周速U [m/s]、ビーズ質量 MGM [kg]、ビーズ径 dGM [m]、ビーズ密度 ρGM [kg/m3]
比エネルギー(投入動力量)
ベッセル内ではビーズが一様な動きをしないため応力数と応力強度には分布がある。これらを合わせると比エネルギー EV (式11)となり、粒子の単位処理量あたりの投入されるエネルギー[J/kg]を表す。

まとめ
応力数と応力強度からビーズミルの粉砕・分散効率に影響を与えるファクターを検討すると、「(1)ビーズ径」「(2)ビーズ充填率」「(3)ビーズ密度」「(4)アジテータ周速(回転数)」「(5)滞留時間」「(6)スラリーの固形分濃度」が挙げられる。
例えば、ビーズミルのアジテータ周速を速くすると応力数と応力強度が大きくなり、ビーズ充填率を高くすると応力数が大きくなる。また、ビーズ径が小さくなると応力数は増えるが、応力強度は小さくなることがわかる。
引用文献
- A.Kwade:Powder Technology、105、382(1999)
- A.Kwade、J.Schwedes:Powder Technology、122、109(2002)
- 神田良照:化学工学、66、11、696(2002)
- 後藤生也:J.Jpn.Soc.Colour Mater.、86、179(2013)
- 石井利博:J.Jpn.Soc.Colour Mater.、81、169(2008)

