粉砕効率の減少を考慮に入れた式^1、2)

一般にKickの法則は粗粒域で、Rittingerの法則は微粉域で適用できるといわれているが、さらに微粉域ではクッショニング現象、ボールへのコーティング現象によって粉砕効率が次第に低下する傾向があり、ある限界の粒度に達したあとは全く粉砕が進まないこともある。このような現象を考慮した粉砕仕事式として、比表面積を用いた式がある。粉砕過程全般に対して生成表面積の変化を示したのが「田中の粉砕限界説（以下、田中の式）」である。
田中の式は、粉砕エネルギーに対する比表面積増加速度が0になる限界比表面積と、そのときの比表面積の差に比例するという仮定より

5式を積分して、S_∞≫S の場合は、6式を得る。

生成する表面積S は粉砕エネルギーW の増大に伴い初期は増加する（Rittinger則）が、やがて増加速度は減少し限界値S_∞ に達することを数式で表示したものであり、粉砕エネルギーW の代わりに粉砕時間t で表することも可能である。
田中の式による粉砕エネルギーと粉砕生成表面積の概念図を示す。

比表面積に限界値が存在する原因として、以下の3つが考えられる。

1. 結晶粒子の限界以上に粉砕できない。
2. 着水分やVander Waals力などによる凝集があり、このため粒子が大きくなる速度と粉砕の速度が平衡する。
3. 微粉は緩衝作用をして粉砕の進行を阻害する。

修正限界比表面積に関する「Harris（ハリス）の式」

生成微粉の影響を考慮した「神保ら³⁾の式」

ここで、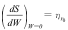
と表わすと、

この式は、

1. 生成新表面が粉砕効率にまったく影響を与えない場合は、
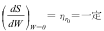
   となってRittinger則となる。
2. 限界比表面積S_∞ が存在する場合、S＝S_∞ で
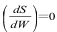
   の場合は、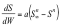
   となり、この式でn ＝1の場合は田中の式となる。
   しかし、実際は粉砕初期においては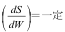
   の領域、つまり、Rittinger域が存在し、その後、6式～8式の関係が表れるようである。

3. 粉砕のエネルギー収支

粉砕は、単に新しい表面が生成するだけでなく、固体表面で結晶構造が変化するなど、化学的、物理化学的変化がある。粉砕による機械的な操作に伴い、物質の化学的変化が生じることを「メカノケミストリー（機械的化学）」という。つまり、生成表面エネルギーと熱発生以外にもこのメカノケミストリーによるエネルギーの出入りが考えられる。
「Rehbinder」と「Chodakow」は、Kickの式（2式）と田中の式（5式）を結び合わせ、さらに、粉砕エネルギーは表面エネルギーの増加と、後に熱エネルギーに変換する弾性エネルギーの蓄積と固体表面の何らかのメカノケミカルな構造変化（塑性変形）に費やされると考え、「Rehbinder-Chodakowの式」を提案している。

Rehbinder-Chodakowの式は、

となる。ここで、右辺第1項はKick則、第2項の括弧の外は田中の式を示し、括弧内の第2項はメカノケミカルな要因を示している。η_m は粉砕の機械効率、αは弾性エネルギーの関するもの、βは固体表面層の物理化学的変化に関するもの、γは表面エネルギーを表わす。

粉砕機のエネルギー収支は非常に低く、ほとんどのエネルギーが熱に変換されるが、その場合、粉体集合体の摩擦係数やメカノケミカルな現象の問題も無視できないことである。このため、特に粉砕機では、粉体の物性を変化させることも粉砕効率、能力の増大に必要となる。

ところで、これらの仕事法則つまり効率の式は、同一粉砕条件のみ使えるため、条件が変わった場合は定数を再び求める必要がある。また最近のように連続式粉砕や閉回路粉砕が主だった方法では、連続的な粒子径変化を前提とした式は使いにくい。その上に超微粉砕の問題になると、S_∞ を大きくするための因子いかにして大きくするか、それに作用する要因は何かを検討しなくてはいけない。

表　粉砕理論の式

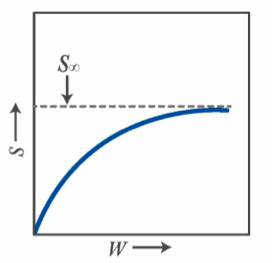
図　田中の式による粉砕エネルギーと粉砕生成表面積の関係¹⁾