技術情報
微粒子技術コラム
理論編
粉砕理論について考える (1)
3つの粉砕理論
「粉砕理論」は、単位操作※)としての粉砕に関する理論であり、「1.物質に関する理論」「2.粉砕操作に関する理論」「3.プロセスに関する理論」の3つに分類される。
1. 物質に関する理論
物質に関する理論には、粒子1個の破壊メカニズムに関する材料力学的研究がある。物質の強度や材料物性を用いた粒子1個の破壊エネルギーの評価、粉砕に投入したエネルギー収支を物理化学的な解析と結び付けていくメカノケミストリーの理論やメカニカルアロイングに代表される、粒子の複合化や表面改質などの研究が相当する。
2. 粉砕操作に関する理論
粉砕操作に関する理論は多岐にわたるが、その主要なものは粉砕のエネルギー消費に関する理論としての「粉砕仕事法則(後述)」がある。これらの関係式は破壊のメカニズムを使い様々な形で理論的導出が試みられている。もう1つの主要な理論が粒子径分布に関するもので、これまでの経験式に対し、破壊機構や確率論的考察から粒子径分布の理論的導出がある。
3. プロセスに関する理論
粉砕プロセスに関する理論としては、粉砕機内の砕料、媒体の動きに関するもの、粉砕と分級、乾燥などの他の単位操作と組み合せたプロセスの開発、また各プロセスのシミュレーションとの比較・検討がある。
粉砕仕事法則を支配する3つの式
ここでは、粉砕理論の基礎となる粉砕のエネルギー消費に関する理論としての粉砕仕事法則について説明する。
粉砕仕事法則1~3)
粉砕では新しい表面が生成され、表面積の増大に伴い、表面エネルギーが増大する。そのために必要な仕事を「粉砕仕事量」、あるいは「粉砕エネルギー」という。単位仕事量W は比表面積⊿S に比例する。この考えは、1867年にRittinger(リッティンガー)によって見出され、「Rittinger則」として知られている。
この法則は、粉砕前後の代表径をx1、x2とし、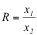 を粉砕比とすると次式のRittinger則となる。
を粉砕比とすると次式のRittinger則となる。

一方、弾性変形に基づくエネルギー則が「Kick(キック)則」(1883年)で、

で表される。
1式および2式を微分式で表すと「Lewis(ルイス)」の一般式が得られる。

Lewisの一般式において、n=2でRittinger則、n=1でKick則になる。
「Bond」は、n=1.5をとって第3法則を提唱した(1952年)。

ここで、Wi は無限大の大きさから100μmまで砕くのに必要なエネルギーで仕事指数(Work Index)とよばれ、種々の砕料に対して多くの粉砕機の実測値に基づき、それらを平均値として計算されたものである。この式のx2 は砕製物80%通過のふるい目の大きさ [μm]である。
完全に均一で等方性の材料の物体に、弾性限界まで少しずつ均一な荷重をかけていくと、圧縮の仕事は弾性的に蓄えられたエネルギーに等しくなり物体の体積に比例する。これはKickの考えである。ところが、加えられたエネルギーがある値(限界ひずみエネルギー)を超えると破壊されて破片になる。このときの割れのパターンにより結果は全く変わってくる。もし物体が均一あるいは等方性でなく、応力集中面をもっていて、ここに全てのひずみエネルギーが集中すれば、生成表面積に比例するというRittingerの考えが成立する。実際には上記の中間のいろいろな場合が存在する。
大まかにいえば、粗粉砕では体積変化に比べて表面積増加が小さくなることからKickの考えが支配的となり、微粉砕では逆に表面積増加が支配的になることから Rittingerの考えが成立する。
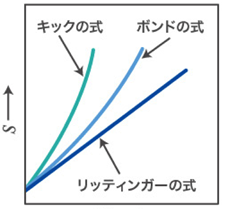
図 粉砕エネルギーと粉砕生成表面積の関係1)
※単位操作とは、製品を製造する際の流体輸送、伝熱、乾燥、蒸留、晶出、抽出、吸着、粉砕、混合、ろ過、遠心分離などのそれぞれの操作(ハンドリング)のことである。
引用文献
- 化学工学協会編:化学工学便覧改訂五版、丸善、p.821(1988)
- (社)日本粉体工業技術協会編:先端粉砕技術と応用、エヌジーティーp.14(2005)
- 工場操作シリーズNO.1 改訂・粉砕、化学工業社、p.1(1969)

